Remapping Keyboard Velocity

19 Apr 2014

As a musician, one of the first things I need to address is the 'feel' of my instruments. I'm sure that down the line, there will be a sweet device for this sort of transformation, but for now, we can do it entirely within Bitwig API.

Revisiting Generic Keyboard Implementation, we have host.getMidiInPort(0).createNoteInput("MIDI Keyboard"); inside init(). This function returns an object of type NoteInput which has the method setVelocityTranslationTable().

var noteInput = host.getMidiInPort(0).createNoteInput("MIDI Keyboard");
noteInput.setVelocityTranslationTable( table );

This method takes an 128 length array, or a hash table, transforming the index of the array into the values of the array as the translation being performed.

So, for example:

var table = [];
table[50] = 127;

would translate a note of velocity 50 into a velocity of 127. This way, a keyboard, like mine, which produces a narrow range of output, generally from 40 to 75, can be expanded to produce the full range of velocities accepted by software instruments. However, BitWig requires a table of 128 points to match every velocity a keyboard can produce with an appropriate transformed value, so we must start with a set of numbers to represent this transformation.

I use the worlds greatest Piano Modelling software PianoTEQ to come up with the following velocity curve.

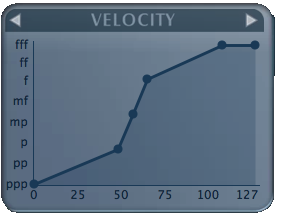
Velocity Curve

Exported from the program, Velocity = [0, 1, 46, 50, 62, 98, 127; 0, 1, 32, 64, 96, 127, 127] gives a nice starting place to do a linear interpolation. The first set of numbers is the input velocities, and the second set, the output. Linear interpolation is a geometry technique to find any point on a line between two points.

 1   var noteInput = host.getMidiInPort(0).createNoteInput('Maschine Midi In');
 2 
 3   inputVel = [ 0, 1, 46, 50, 62, 98, 127 ]; // x
 4   transVel = [ 0, 1, 32, 64, 96, 127, 127 ]; // y
 5 
 6   var output = [];
 7   for ( slope = 0, i = 0; i < 128; i++){
 8     //Y = Y1 + ( ( Y2 - Y1) ( X - X1 ) / ( X2 - X1) )
 9     y = transVel[0] +
10       ( ((transVel[1] - transVel[0]) * ( i - inputVel[0] )) /
11       (inputVel[1]-inputVel[0])
12     );
13     output[i] = Math.min(Math.round(y), 127);
14     if ( inputVel[1] < i ){
15       transVel.shift();
16       inputVel.shift();
17     }
18   }
19 
20   noteInput.setVelocityTranslationTable(output);

We iterate through inputVel and transVel by shifting each array every time the x or i reaches the next value of inputVel. This shift makes the operation on lines 9-13 apply again, with the new values at [0] of each array.

I would highly recommend you just copy and paste this code into your application and change as you see fit, but this is how it's done.

Adventures Programming BitWig API

Remapping Keyboard Velocity